Децибелы ЭТО ОЧЕНЬ ПРОСТО!

Ю.БАЛТИН (YL2DX),

г.Рига.

Когда требуется сравнить какие-нибудь величины, это можно сделать по-разному. Можно, например, разделив эти величины одну на другую, сказать — Р₁ больше чем Р₂ в 3 раза, или Р₁, меньше чем Р₂ в 28 раз. Если нам понадобится далее вести какие-то расчеты, мы будем пользоваться отвлеченными числами 3, или 28, или 1/28 (иногда для уточнения добавляя слово "раз").

В ряде случаев для расчетов или для большей наглядности сравнения оказывается удобнее логарифмировать отношение величин и оперировать далее с числом log_а(Р₁/Р₂). Известно, что применение логарифмов упрощает математические расчеты, в частности, позволяет вместо умножения и деления пользоваться сложением и вычитанием. При большом диапазоне изменений какой-либо величины логарифмический масштаб позволяет лучше разглядеть на одном и том же графике и малые, и большие ее относительные изменения.

Чтобы различать, имеем ли мы дело с числом "раз" или с его логарифмом, а также чтобы зафиксировать, каким основанием мы пользуемся при логарифмировании (числом 10, числом e=2,71828 или иным), следует присвоить этому логарифму какое-нибудь название. В системе СИ в качестве относительной логарифмической единицы отношения мощностей Р₁, и Р₂ принят десятичный логарифм Ig(Р₁/Р₂). Эта единица называется бел (Б).

На практике этой довольно крупной единицей оказалось не очень удобно оперировать, поэтому ее "разменивают" на единицы, в десять раз меньшие — децибелы. Соотношение двух уровней мощности Р₁ и Р₂ в децибелах (дБ, или dB) выражают по следующей формуле:

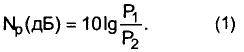
Множитель 10 в формуле (1) появился потому, что десять децибел как раз и есть один бел. Таким образом, не повезло изобретателю телефона А.Г.Беллу — мало того, что единицу его имени укоротили на одну букву "л", так еще и пользуются лишь десятыми долями.

Теперь разберемся с отношениями напряжений или токов. Вспомним из школьного курса, что мощность в линейной цепи равна:

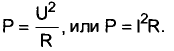
Отсюда легко видеть, что:

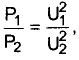
а значит:

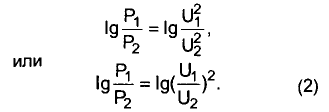
Из школьного же курса вспомним:

Из равенств (2) и (3) вытекает следующее:

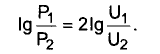
Это и есть формула взаимосвязи между "белами по мощности" и "белами по напряжению" в одной и той же цепи, если в ней выполняется закон Ома. Ну, а если мы намерены пользоваться десятыми долями бела, то обе половины этого уравнения необходимо умножить на 10. Отсюда следует, что при сравнении величин напряжений (U₁ и U₂) или токов (I₁ и l₂), их соотношение в децибелах:

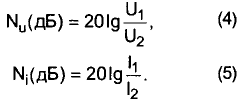
Полезно запомнить несколько характерных значений, приведенных в таблице.

Если напряжение на резисторе увеличить вдвое (на +6 дБ "по напряжению"), то и протекающий через него ток увеличится вдвое (на +6 дБ "по току"), а мощность, выделяемая этим резистором, станет вчетверо больше—опять-таки на +6 дБ ("по мощности"). Чтобы уменьшить мощность в 10 раз (-10 дБ), нужно снизить приложенное к резистору напряжение в 3,162 раза (-10 дБ), отчего ток по закону Ома тоже уменьшится в 3,162 раза (-10 дБ).

Поскольку мощность в линейной цепи пропорциональна квадрату напряжения или тока, численные значения соотношений их величин, выраженные в децибелах, остаются одними и теми же как при сравнении мощностей, так и при сравнении напряжений или токов:

В случае ослабления сигнала (когда отношение Р₁/Р₂ меньше единицы), логарифм становится отрицательным, следовательно, отрицательным становится и коэффициент передачи данной цепи, выраженный в децибелах. Для вычисления общего коэффициента передачи нескольких последовательно соединенных цепей или устройств достаточно просуммировать значения в децибелах с учетом их знаков (+) или (-). Это

намного удобнее, чем перемножать исходные значения в разах.

При вычислении коэффициента передачи различных устройств (например, усилительного каскада) во многих случаях мы имеем дело с разными входным и выходным сопротивлениями; в нелинейных цепях напряжение и ток взаимно не пропорциональны, а мощность не связана с тем и другим квадратичной зависимостью. Коэффициенты передачи таких цепей по току:

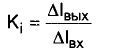
и по напряжению:

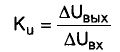
различны и в разах, и в децибелах; коэффициент передачи по мощности:

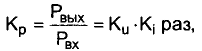
а в децибелах:

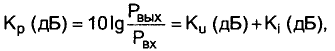
поскольку

Равенство (6) к этим случаям не относится, но по отдельности изменения или соотношения величин тока или напряжения на одном и том же линейном сопротивлении (например, на сопротивлении нагрузки нелинейного усилителя) все равно выражаются в децибелах формулами (4) и (5), а изменения уровня мощности — формулой (1).

Зачем возиться с логарифмами? Во-первых, логарифмическая шкала наиболее естественна для наших органов чувств, в частности, для слуха. Закон логарифмической зависимости ощущений от силы воздействия сформулирован Вебером и Фехнером (обычно называется законом Вебера) — "одинаковые относительные изменения раздражающей силы вызывают одинаковые приращения слухового ощущения, т.е. слуховое ощущение пропорционально логарифму раздражающей силы".

Практически, 1 дБ — это наименьшая ступенька изменения интенсивности звука, едва обнаруживаемая на слух, изменение на 6 дБ воспринимается на слух как хорошо заметное (но небольшое — примерно вдвое громче), на 10 дБ — значительное, а на 20 дБ—как весьма большое. Каждый балл по шкале S системы RST — это 6 дБ (или 0,6 бела), так что мы, особо не задумываясь, занимаемся логарифмированием каждый раз, когда начинаем очередную связь в эфире, передавая рапорт корреспонденту.

Во-вторых, значения величин, с которыми нередко приходится сталкиваться, в обычном исчислении бывает трудно соразмерить—скажем, 1 микровольт отличается от 1 киловольта в 1 000 000 000 раз. А в децибелах разница выражается вполне удобной величиной 180 дБ. Мощности, которые выделятся на одном и том же сопротивлении при приложении к нему этих напряжений, будут отличаться астрономически — в 1 000 000 000 000 000 000 раз, а в децибелах — все на те же 180 дБ. С другой стороны, если, например, сравнивать 1,03 мА и 1,37 мА, то их отличие выразится вполне заметной величиной — 2,5 дБ.

Если запомнить характерные значения из таблицы, то можно очень легко пересчитывать в уме и любые другие величины отношений в децибелы и обратно. Например, 4 дБ—это (3 дБ +1 дБ). Значит, отношение мощностей (2x1,26)= 2,52 раза или отношение напряжениий (1,41 х 1,12) =1,6 раза. Или, к примеру, отношение двух значений тока равно 17 раз, то есть (10x1,7). 10 раз по току — это 20 дБ, а 1,7 раза — между 1,41 и 2, значит, где-то около 4,5 дБ. В сумме (20 дБ + 4,5 дБ) = 24,5 дБ. Ну, а для чисел, кратных десяти, мнемоника очевидна.

Децибелы сами по себе — это величины не физические, а абстрактные, математические, такие же относительные, как и разы. Их нельзя пощупать руками как килограмм, метр или киловольт (нет... руками его, пожалуй, не стоит щупать... Hi). Их можно только вычислить, сравнивая реальные физические величины, и оперировать ими при расчетах. Но если мы устанавливаем в качестве эталона 0 дБ какое-то определенное значение физической величины, например, 1 Вт или 1 мкВ, то можем и прямо измерять в децибелах относительно него уровни мощности или, соответственно, напряжения. Обозначают такие единицы измерения теми же буквами "дБ", но с добавлением индекса: дБВт (децибел-ватт), дБмкВ (децибел-микровольт) и т.п. Например, мощность 27 дБВт—это то же самое, что 500 Вт, а -13 дБВт — 50 мВт. Напряжение -3 дБмкВ — 0,707 мкВ, а 23 дБмкВ — 14,14 мкВ.

В акустике за 0 дБ однозначно принято пороговое звуковое давление 2-10 Па, и децибел без дополнительного индекса прямо используется в качестве единицы уровня звукового давления.

На коротких волнах, по системе оценки сигнала RST, напряжение, равное 50 мкВ, на 50-омном входе приемника (S=9), в сущности, принято за ноль децибел. Каждый балл ниже девяти — это -6 дБ (в 2 раза меньше) от этого напряжения, а если сигнал сильнее, то S-метр покажет, на сколько децибел. Чтобы напряжение на входе приемника изменилось на 1 балл, нужно на столько же изменить мощность передатчика — на 6 дБ, то есть в 4 раза. Если получен RS 59+20 dB, то можно (и нужно бы!) смело уменьшать мощность передатчика на 30 дБ (т.е. в 1000 раз!!!) — все равно будет слышно достаточно громко — больше чем на S=7 (с запасом +2 дБ) (конечно, если "+20" было сказано не ради красного словца.. .Hi).

Надеюсь, что теперь понятно, почему "выжимать" 250 Вт из 200-ваттного передатчика просто глупо — увеличение силы сигнала менее чем на 1 дБ вообще никто не заметит, а вот сплэттер или щелчки по всему диапазону вполне реально могут испортить настроение многим.

О чувствительности приемника и S-метра

Чувствительность приемников часто измеряют в децибел-милливаттах (дБм) или дБмВт: 1 мВт = 0 дБм.

В сущности, измерять чувствительность в единицах мощности имеет больше смысла, чем в единицах напряжения, так так нам приходится иметь дело с сигналами разной формы — синусоидальными, шумовыми, шумоподобными и др. К тому же, мы избавляемся от необходимости уточнять, каково входное сопротивление приемника, и имеем возможность сравнивать чувствительность приемников с различными входными сопротивлениями. Эффективное напряжение 50 мкВ на 50-омном входе соответствует мощности -73 дБм. Этой же мощности соответствует напряжение 61,2 мкВ на 75-омном входе. Все это соответствует оценке S=9 сигнала по системе RST на частотах ниже 30 МГц. На УКВ за S=9 принята мощность -93 дБм (5 мкВ на 50-омном входе приемника).

Система оценки сигнала на слух по коду RST была предложена W2BSR в середине 30-х годов и с тех пор стала всемирно признанной. Стандарт градуировки S-метров был установлен IARU в 60-х годах, но когда его принимали, похоже, что ориентировались на не очень чувствительные приемники, а может быть, и на "тугоухих" операторов... (Hi). Впрочем, в те годы еще широко использовалась амплитудная модуляция (AM), в CW-приемниках сравнительно редко встречались хорошие узкополосные фильтры, а собственные шумы радиодеталей были побольше чем сейчас, так что чувствительность среднего любительского приемника была на порядок хуже, чем у современного.

Пороговая чувствительность порядка -130 дБм — очень высокая, но не редкая для современного КВ-приемника при узкой полосе в режиме CW (0,035 мкВ на 50-омном входе). Эта величина ниже, чем S=1 (-121 дБм) по S-метру. При таких уровнях имеется несоответствие слуховой (по таблице значений "S") и инструментальной (по S-метру) оценки силы сигнала — в чистом эфире, без помех, на хорошем приемнике сигнал с уровнем -125 или -130 дБм может вполне восприниматься на слух как хорошо читаемый "слабый", или "очень слабый" т.е. S=3 или S=2, a S-метр не будет показывать ничего. Но, по сути системы RST, если S=0, то сигнала просто не слышно совсем, a S=1 — это, по определению, "едва ощутимый сигнал". В тех же условиях сигнал мощностью -85 дБм может выглядеть как очень громкий (при достаточном коэффициенте усиления УНЧ приемника), но S-метр покажет не 9, а только 7 баллов — это типично, например, на 10-метровом диапазоне (впрочем, он как раз на границе KB и УКВ, где шкалы S-метров разные).

В трансиверах разных фирм стандарт IARU не очень-то соблюдается. Кроме того, чувствительность одного и того же приемника на разных диапазонах различается и может ступенчато регулироваться оператором (включением или выключением преду-силителей ВЧ и аттенюаторов), а шкала S-метра остается одна на все случаи. Если включен аттенюатор, то следует величину его затухания прибавить к показаниям S-метра, а если включен дополнительный пре-дусилитель — то величину его усиления из показаний S-метра вычесть. Разумеется, это относится только к случаю использования для приема полноразмерных согласованных антенн. Когда действующая высота антенны мала, или антенна не согласована со входом приемника, показания S-метра сами по себе ничего не скажут о реальном уровне сигнала в эфире.

В сущности, единственной полной и действительно объективной характеристикой уровня сигнала, создаваемого каким-либо передатчиком в точке приема, является напряженность поля, которую можно вычислить, разделив ЭДС на клеммах приемной антенны U_A на ее действующую высоту h_д:

Действующая высота (или действующая длина) антенны вычисляется по формуле:

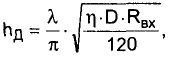
т.е. зависит от длины волны l , коэффициента направленного действия D, КПД (?) антенны и ее входного сопротивления (идеальный полуволновой диполь в свободном пространстве имеет действующую длину l /?). Поэтому, если нужно более точно охарактеризовать силу сигнала от какой-либо станции, код RST надо дополнить сведениями об используемой приемной антенне и сообщить, показания ли это S-метра или оценка сделана на слух.

КВ и УКВ №4, 2001 г.